Abstract:

Recent new interest in modelling the protein-solvent interactions by continuum methods lead to several improvements for calculating the solvent accessible surface area and its derivative [1]. One of the most efficient analytical method is a parametric approach based on the Gauss-Bonnet theorem. This approach has been implemented as molecular surface routine PARAREA [2] in the energy minimization and Monte Carlo simulation package FANTOM [3].

In this study we demonstrate that this approach can be further enhanced by avoiding the calculation of a relatively large number of potential intersection points in the Gauss-Bonnet path. PARAREA finds them by a straightforward test of all atom pairs in the neighbor list of each atom. Numerical tests showed that this part of the routine consumes a significant portion of the execution time. The new surface routine GETAREA efficiently finds the solvent exposed vertices of the Gauss-Bonnet path by calculating the intersection of half-spaces (IHS). These half-spaces are defined by the planes of two-sphere intersection. Geometric inversion conveniently transforms intersection planes into a set points in dual space. Convex hull of these points corresponds to the desired IHS [4]. Finally, the vertices of Gauss-Bonnet path are found by intersecting edges of IHS with the central atom sphere. Additionally, the list of neighbor atoms is obtained with the aid of a cubic lattice algorithm, as opposed to direct search in PARAREA.

Numerical tests with several conformations of the peptide Met-enkephalin and the medium-size protein tendamistat show the correctness of the area and gradient calculation. The CPU time spent in GETAREA has been significantly reduced by factors of 0.4 (Met-enkephalin) and 0.6 (tendamistat) as compared to PARAREA. With the improved performance of the method we are currently performing search for low energy conformations of peptides in solution and apply the improved version of FANTOM in studies of protein folding.

References

1: W. Braun, ''Incorporation of Solvation Energy Contributions for Energy Refinement and Folding of Proteins'' in Computer Simulation of Biomolecular Systems, Vol.3 (van Gunsteren, W.; Weiner, P.; Wilkinson, T. Eds.), ESCOM, Leiden, 1996 (in press).
2: Ch. Mumenthaler and W. Braun, J. Mol. Mod., 1, 1 (1995).
3: B. von Freyberg and W. Braun, J. Comp. Chem., 14, 510 (1993).
4: F.P. Preparata and M.I. Shamos, Computational Geometry: An Introduction, Springer-Verlag, New York, 1985.

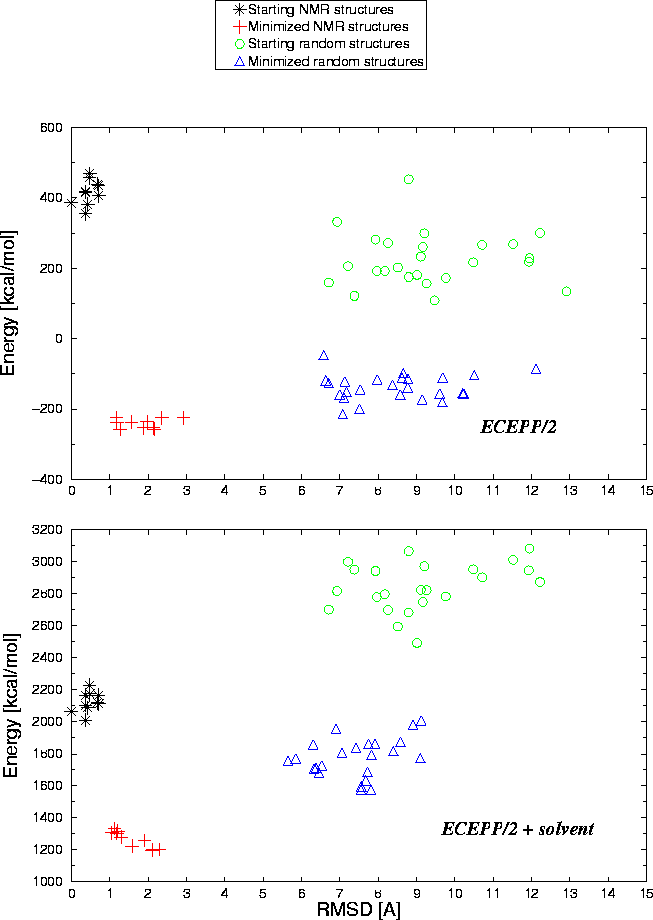
Protein-Solvent Interaction Energy:

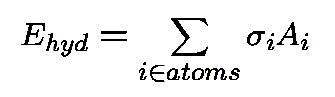
_i: : atomic solvation parameter;
A_i: : solvent accessible surface area (ASA);

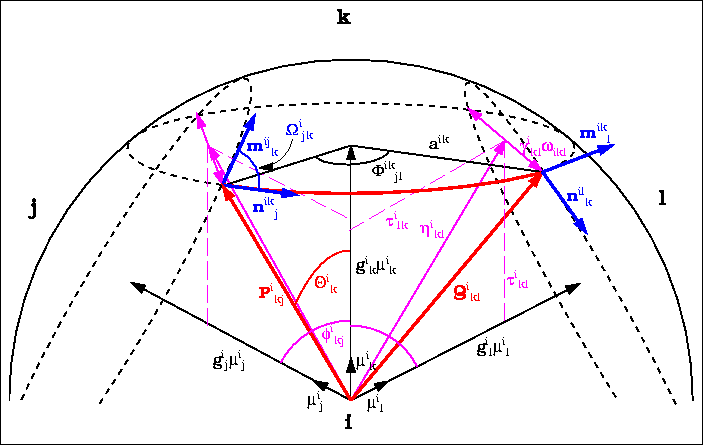
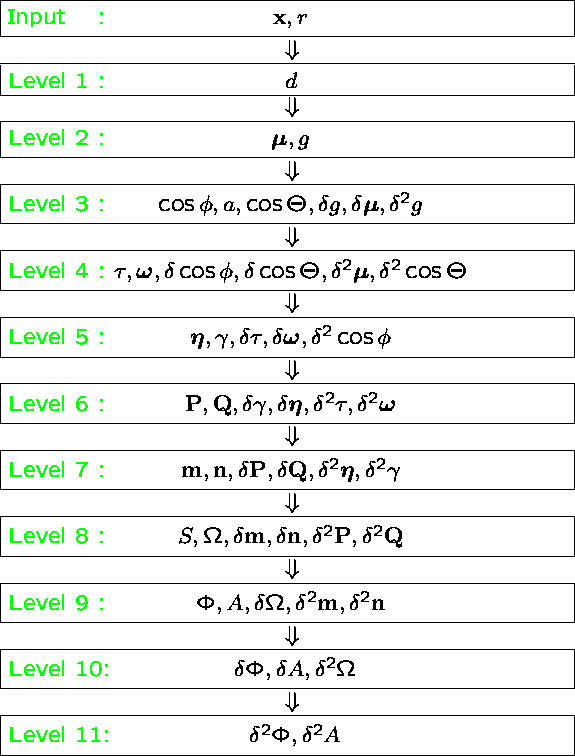
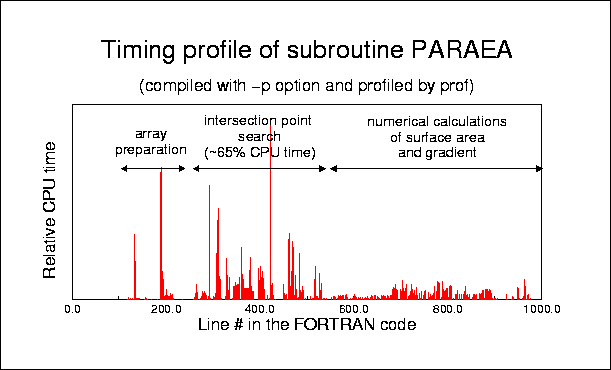
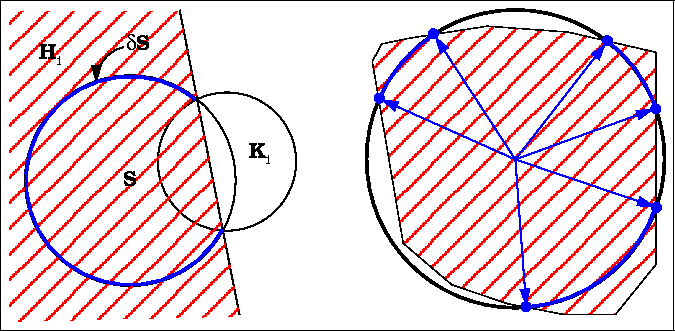
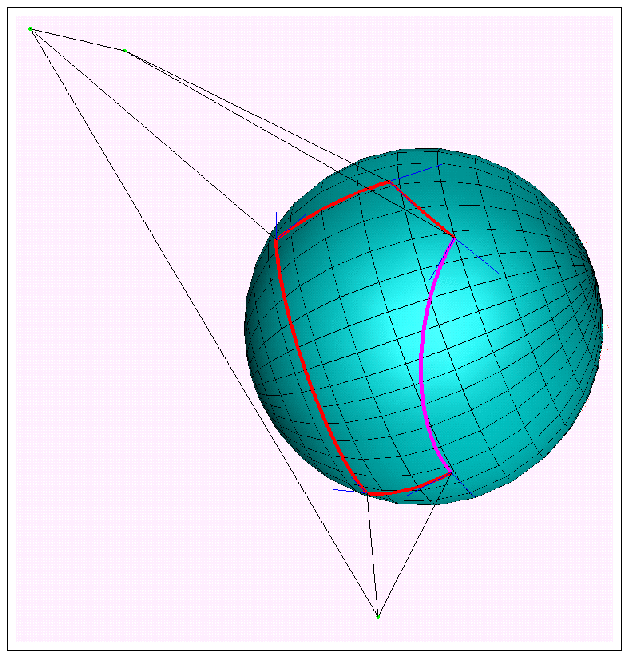
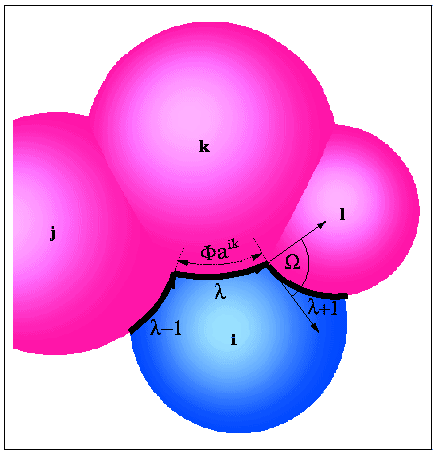
ASA and its derivatives can be calculated analytically from Gauss-Bonnet theorem:

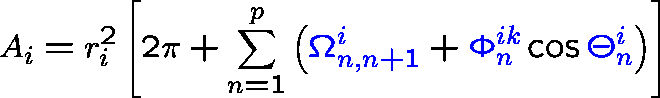
p: : number of intersecting arcs defining ASA;
r_i: : radius of the i-th sphere;

ⁱ _n,n+1 : angle between tangential vectors;

^ik_n: : angle defining arc length;
ⁱ_n: : polar angle of the ik-th intersection circle;
a^ik: : radius of the ik-th intersection circle.

New Vector Parametrization of Accessible Arcs

Definitions:

x_i : Cartesian coordinates of atom i;

xⁱ_k = x_k-x_i ; dⁱ_k = |xⁱ_k| : interatomic distance vector and its length;

µⁱ_k = xⁱ_k/dⁱ_k : unit vector along xⁱ_k ;

gⁱ_k = [(dⁱ_k)² + r_i² + r_k²]/[2dⁱ_k]: distance to the center of the ik-th intersection circle;

n^ik_j = [µⁱ_k×Pⁱ_kj]/a^ik ; m^ik_l = [µⁱ_k×Qⁱ_kl]/a^ik : tangential unit vectors;

S^ik_jl = sign[µⁱ_k· (n^ik_j×m^ik_l)] : orientation of the tangential vectors.

Flowchart illustrating algorithmic calculation of accessible surface area and its partial derivatives

( denotes partial derivative with respect to the relative Cartesian coordinates)

Problem : find all accessible arcs = find all relevant intersection points P and Q

Solution implemented in routine PARAREA: find all vectors P, Q and eliminate those that are buried by other neighbor atoms.

Trouble : this algorithm is highly CPU-time consuming:

New solution implemented in routine GETAREA: relevant P, Q can be determined from 3D half-space intersection. Simple 2D example illustrates this concept:

Two intersecting spheres, S and K_i, define a half-space H_i. Surface of S, S, intersected with H_i gives accessible surface, A_i (marked in blue), i.e., part of S that is not buried in K_i:

If sphere S has N neighbors, then its accessible surface is given by S crossed with intersection of all N half-spaces:

Half-space intersection is a polyhedron (called here the "IHS polyhedron") whose edges cross S at exactly the desired points P and Q.

In 3D the vertices of Gauss-Bonnet path are points where edges of the IHS polyhedron cross the sphere surface:

Finding the IHS polyhedron of N half-spaces from a convex hull using the power of computational geometry. Some useful definitions: Geometric inversion in 3D Euclidean space is a point-to-point transformation of E³ which maps a point with spherical polar coordinates (R, , ) to the point with coordinates (1/R, , ). Convex hull. Given a finite subset L of points of E³, the convex hull of L, is the smallest convex polyhedron containing L.

	Step 1: find distance vectors (red) to every halfspace boundary and transform them by geometric inversion (blue).
	Step 2: find convex hull (blue) of transformed points. Find distance vectors (green) to the faces of convex hull.
	Step 3: geometric inversion of green vectors yields vertices (black) of the IHS polyhedron (red).

Performance of Surface Routines Systems studied: Met-enkephalin; 5 amino acid residues. Tendamistat; 74 amino acid residues. Method: elapsed CPU time (as reported by SGI FORTRAN function DTIME) spent in conjugate gradient energy minimization. Hardware: Silicon Graphics Indigo² with 195 MHz MIPS R10000 CPU.
Molecule	Met-enkephalin		Tendamistat
Routine	PARAREA	GETAREA	PARAREA	GETAREA
Total CPU time [s]	33.4	17.8	823	437
CPU time spent in surface routine [s]	26.0	11.1	573	182
Number of routine invocations	1302	1215	1349	1382
CPU time per invocation [s]	0.020	0.009	0.425	0.132
Ratio (P/G)	2.22		3.22

Application: folding studies of the pheromone Er-10 from Euplotes raikovi (38 amino acid residues).

Ten tertiary structures of Er-10 were solved by NMR spectroscopy.
Three-helix bundle (residues 2-8, 12-18 and 24-32) stabilized by three disulfide bridges.
Energy minimization calculations were performed with and without protein-solvent interactions. Apolar solvation parameters were used ( _i = 1 kcal/mol/Å² for C and S; = 0 kcal/mol/Å² for other atoms).
Helical residues constrained to -72° < < -42° and -62° < < -32°. S-S bridges not included.
All 10 unrefined NMR structures and 25 random structures used as starting geometries.
RMSD values calculated for backbone atoms. Unrefined NMR structure 1 used as reference.

Conclusions:

Analytical calculation of the solvent accessible surface areas and their derivatives (ASAD) has been simplified due to the new vector parametrization.
CPU time spent on ASAD calculations can be greatly reduced by employing new algorithm of finding the vertices of Gauss-Bonnet path by calculating the intersection of half-spaces.
Protein-solvent interaction is an extraordinarily important factor in computational studies of protein folding. Energy minimization without solvent is successful in mathematical sense, but it does not allow one to find the native structure. On the other hand, inclusion of solvent smoothes low energy local minima for unfolded structures and therefore drives structure minimization towards a folded state.

​Abstract:

​References

​Protein-Solvent Interaction Energy:

​New Vector Parametrization of Accessible Arcs

​Definitions:

​Flowchart illustrating algorithmic calculation of accessible surface area and its partial derivatives

​Performance of Surface Routines

​Conclusions: